• I. Matlab Toolbox

• Download the file ‘NA-MEMD.zip’ for the latest version. It includes three matlab functions, ‘read_me.txt’, ‘namemd.m’ and ‘add_noise.m’. The main function is ‘namemd.m’, which calls ‘add_noise.m’ to specify the noise channels. For more details, please refer to ‘read_me.txt’.

• II.Example

  x = randn(1000,3);
  ndir = 64;
  stp_crit = 'stop';
  stp_vec = [0.075 0.75 0.075];
  mode = 'na_fix';
  intensity_noise = 1;
  n_channel_na = 3;
  imfs = namemd(x, ndir, stp_crit, stp_vec, mode, intensity_noise, n_channel_na);

  III.Copyright

  Yuexin Wen, Yi Zhang, Peng Xu, Steven Su, Limei Xu, and Dezhong Yao (October 2017).

I. Orignial Paper

1. Zhang, Yi and Xu, Peng and Li, Peiyang and Duan, Keyi and Wen, Yuexin and Yang, Qin and Zhang, Tao and Yao, Dezhong (2017). Noise-assisted multivariate empirical mode decomposition for multichannel EMG signals. Biomedical engineering online, 16(1), 107.

2. Zhang, Y., Su, S., Xu, P., & Yao, D. (2017, July). Performance evaluation of Noise-Assisted Multivariate Empirical Mode Decomposition and its application to multichannel EMG signals. In Engineering in Medicine and Biology Society (EMBC), 2017 39th Annual International Conference of the IEEE (pp. 3457-3460). IEEE.

II. Other Reference

1. Rehman and D. P. Mandic, "Multivariate Empirical Mode Decomposition", Proceedings of the Royal Society A, 2010.

2. G. Rilling, P. Flandrin and P. Goncalves, "On Empirical Mode Decomposition and its Algorithms", Proc of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing, NSIP-03, Grado (I), June 2003.

3. N. E. Huang et al., "A confidence limit for the Empirical Mode Decomposition and Hilbert spectral analysis", Proceedings of the Royal Society A, Vol. 459, pp. 2317-2345, 2003

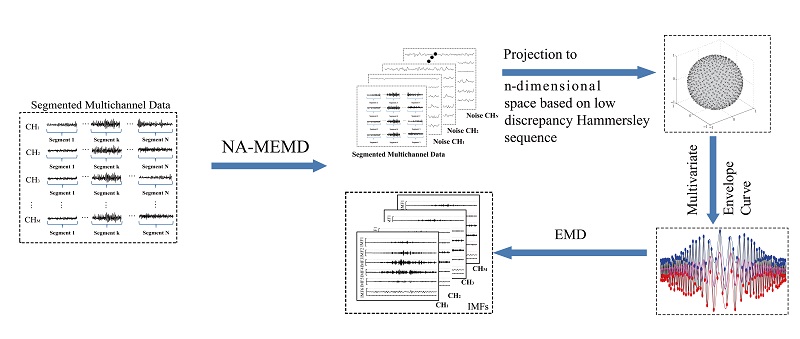
Empirical Mode Decomposition (EMD)-based approaches have been popularized in biosignal processings such as Electroencephalograph (EEG), Electromyography (EMG), and Functional Magnetic Resonance Imaging (fMRI). Ensemble Empirical Mode Decomposition (EEMD) was widely used for single-channel-based signal processing as it can effectively extract the temporal information of time series. However, it cannot well address the temporal and spatial characteristics in relation to multichannel signals. Accordingly, the multivariate extension of EMD (MEMD) has been developed to deal with multichannel biosignals, specifically for the applications of EEG-based brain-computer interface as well as researches on fMRI.

Our previous studies concerned about the use of Noise-assisted multivariate Empirical Mode Decomposition (NA-MEMD) for the preprocessing of multichannel biosignals such as EMG. A comparative study is provided by assessing EEMD, MEMD, and NA-MEMD. The outcomes from these approaches are then quantitatively estimated on the basis of three criterions, the number of Intrinsic Mode Functions (IMFs), mode-alignment and mode-mixing. Results showed Both MEMD and NA-MEMD methods (except EEMD) can guarantee equal numbers of IMFs. For mode-alignment and mode-mixing, NA-MEMD is optimal compared with MEMD and EEMD, and MEMD is merely better than EEMD.

The Matlab code for NA-MEMD has been provided for free downloads.