If you fail to run the emiCCA toolbox, please try to install JAVA in your computer to make MATLAB can run JAVA code. More details of the toolbox description can be seen in “read me.txt” file in the package.
The MINE information can be seen in MINE_info.zip.
MINE_info.zip
Here we show the results of emiCCA and CCA considering nonlinear relationship (y_1=cos(2πx_1), sample size is 500, dimension = (6, 4) and IID noise = 0.05 STD). More details can be seen in “examples_of_emiCCA.m” file in the emiCCA toolbox.
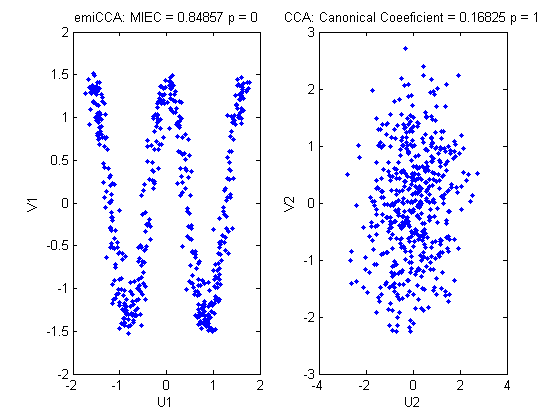
Fig. 1: Results of emiCCA and CCA under nonlinear condition.
"Characterizing nonlinear relationships in functional imaging data using eigenspace maximal information Canonical Correlation Analysis (emiCCA)". Li Dong, Yangsong Zhang, Rui Zhang, Xingxing Zhang, Diankun Gong, Pedro A. Valdes-Sosa, Peng Xu, Cheng Luo, Dezhong Yao*. NeuroImage, 2015, Accepted.
To be continue…
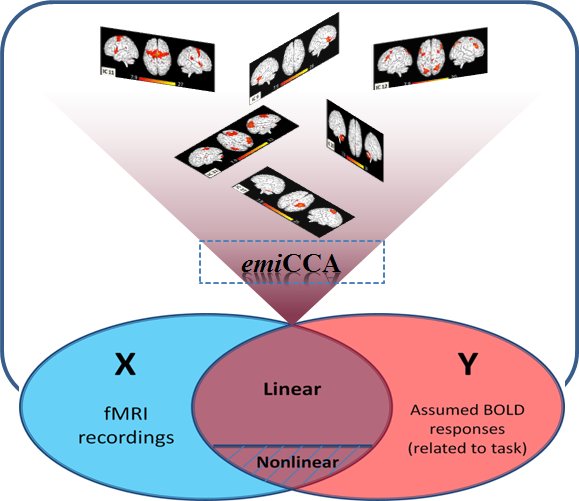
Many important problems in the analysis of neuroimages can be formulated as discovering the relationship between two sets of variables, such as the relations between the X matrix comprising the time courses of a spatial independent component analysis (spatial ICA) of task-related fMRI data, and the Y matrix of time courses of assumed BOLD response (the design matrix). The linear techniques such as canonical correlation analysis (CCA) have been commonly used. However, to further explore potential nonlinear processes that might co-exist with linear ones in brain function, a more flexible method is required. Here, we propose a new unsupervised and data-driven method, termed the eigenspace maximal information Canonical Correlation Analysis (emiCCA), which is capable of automatically capturing the linear and/or nonlinear relationships between various data sets.
More details about the emiCCA can be seen in our original paper, and it may be a promising technique for exploring various data.